試験問題の評価方法　IRT（項目反応理論）分析はどのように活用できるか？

CBTをはじめとする資格試験では、試験結果データが蓄積されるほど「問題の品質管理（出題の妥当性・公平性）」を高い解像度で行えるようになります。平均点や正答率だけでも一定の改善は可能ですが、「どの能力層に対して、その問題がどんな働きをしたか」まで踏み込むなら、IRT（Item Response Theory：項目反応理論）が有力です。 

IRT（項目反応理論）は、①問題の特性と、②受験者の能力（潜在特性）を、解答データを使い統計モデルで推定する手法です。 

IRTを利用していくことで、試験問題の品質改善や、将来的には、ストックされた問題バンクから自動出題、CAT（適応型テスト）にまでつながる基盤を作れます。CBTのように受験者ごとに出題が異なる場合でも、共通問題等を用いた「IRTに基づく等化」を適切に設計することで、異なる問題を受けた受験者同士でも同一尺度で能力を比較・評価できるようになります。 

このブログが、IRTに関心を持ち、ご検討するきっかけになれば幸いです。 

これまでは平均点・得点分布・正答率・選択肢選択率などで問題を評価することが一般的であり、これは運用上とても重要です。 一方で、これまでの評価方法では、以下のような「限界」が出やすくなりますので、これまで行ってきた評価方法に加え、IRT分析も併用することで、より精度の高い分析・評価を行えます。 
 
これまでの評価方法は古典的テスト理論（Classical Test Theory）と呼ばれています。 

限界①：能力層ごとの「効き方」が見えにくい 

正答率が同じ50%でも、「上位層と下位層がきれいに分かれて50%なのか」「どの層も半々で当たっている50%なのか」で、問題としての価値はまったく違います。 

IRTでは、「受験者の能力値別の正答率」をグラフで見える化することができ、その問題が、どの能力層の受験者に対して効果を発揮しているのかを確認できます。 

ここで重要なことは、IRTでは、正答数（素点）だけでなく、「どの問題に正解し、どの問題で不正解だったか」という反応パターンを考慮して能力θを推定します。そのため、同じ50点でも、より困難度が高い問題に正答している受験者の方が、より高い能力を持っていると推定されるといった評価が可能になります。 

限界②：素点主義の不公平が起きやすい 

これまでの評価方法は、受験者全員が同一問題であることを前提としています。しかしCBT試験では、受験期間が複数日にわたったり、問題セットが複数になったり、問題バンクからランダム出題したりしますので、全員が同一問題が出題されるとは限りません。 

すると「たまたま難しい問題セットを引いた」などで、素点（正答数）だけの採点ではフェアさが崩れやすくなります。IRTは、この課題に対して等化（equating）という考え方の基礎データとなります。これにより、異なる問題セットを受験した場合でも、同一尺度で比較できるようになります。 

IRT分析は試験の分野以外でも利用されており、いくつかの統計モデルがありますが、試験問題（択一式）をIRT分析する場合は、二値反応モデルを使います。二値反応モデルにも1PL、2PL、3PL、4PL、その他と細分化され、一般的には2PLまたは3PLが利用されます。 

2PL（2パラメータ・ロジスティックモデル）：[識別力 a] と[困難度 b] と[受験者の能力値θ]を推定します。 

3PL（3パラメータ・ロジスティックモデル）：2PLに加え[当て推量 c] を推定します。 

[識別力 a] 受験者の能力差をどれだけ見分けられるかを示す指標です。値が大きいほど、成績差が明確になる問題と言えます。 

[困難度 b]どのくらいの能力を持つ受験者が正解できるかを示す指標です。具体的には、正答確率が50%付近（2PLモデルでは50%ちょうど）となる能力値θを表します。値が高いほど、難しい問題と言えます。 

[当て推量 c ]実力が十分でない受験者でも、当てずっぽう等で正答してしまう確率の影響を表します。単純な当てずっぽうなら「1/選択肢数」程度が目安になりますが、設問の作りによって上下します。 

[受験者の能力値θ]能力値θは直接観測できない潜在特性で、推定結果は平均0・標準偏差1などの尺度に変換して扱うのが一般的です。θの理論上の範囲は広く（-∞～∞）、実務では目安として-4～4程度で表現します。 

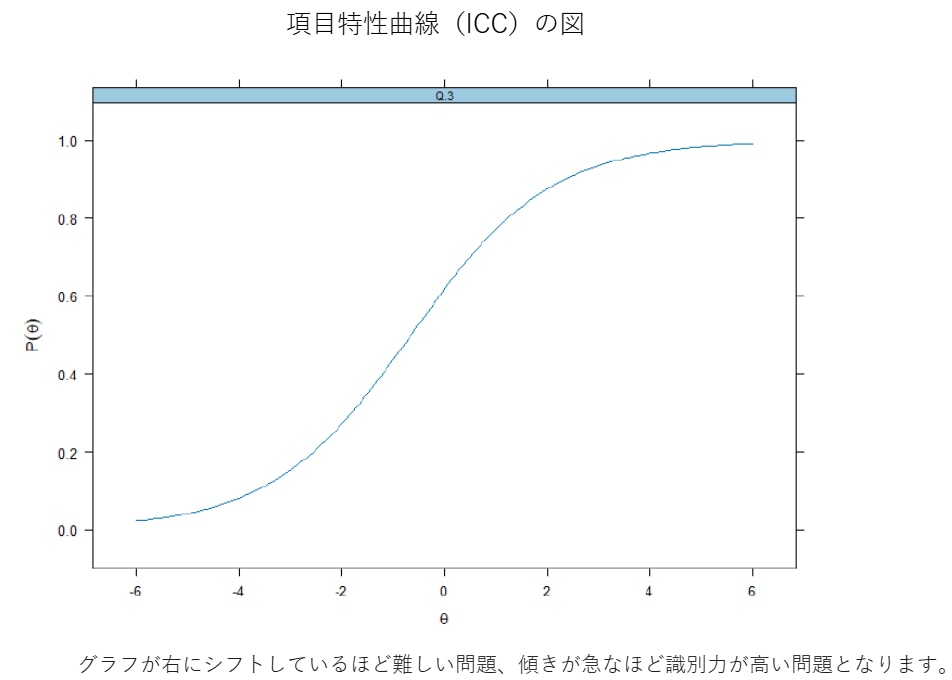
[項目特性曲線 ICC]横軸は受験者の能力値で、グラフ中央θ=0が標準的な能力の受験者となり、θが高いほど正答確率が上がる様子を表します。一般にθ=b付近で正答確率が大きく変化しやすく、その付近での“曲線の鋭さ”が識別力aに関係します。 
※以下の図はbが0付近の例です。 
縦軸は正答率（正答確率）で、受験者の能力が高ければ正答率が高くなります。以下のグラフでは、θ=0付近で傾きが最も大きくなっています。これは、この付近の受験者のわずかな能力差で正答確率が大きく変化していることを意味します。 

まとめると、IRTは「問題の性質」と「受験者の実力」を同じ物差しで整理し、試験をより公平に・継続的に改善するための分析手法です。 

注１：同じ2PL/3PLでも、推定法などの設定により、推定値が多少変わることがあります。外部委託時は、モデル（2PL/3PL）、推定法などを事前に明確化し、継続運用では同一条件で再分析することが重要です。 

注２：解答データ数が少ないと推定値の信頼性が低下します。目安として、2PLは500名程度から、3PLは1000名以上が望ましいとされることが多い一方、必要数は前後し、項目数・難易度の分布・欠測の多さなどで変わります。特に3PLモデルは推定が不安定になりやすいため、十分なサンプルサイズが確保できない場合は、まずは2PLモデルから検討するのが現実的です。 

ストックされた多数の問題から出題（=受験者ごとに問題が異なる）しても、IRTで得られた値を活用し、（共通問題などを用いた）等化を行うことで、同一尺度で評価・判定することや、CAT（適応型テスト）の実現などが、最終的な活用目標となります。 

しかし、今回出題した問題はどうだったかの評価のための資料としても十分利用できます。例えば、項目特性曲線の形に異常は無いか。項目特性曲線を重ねて出題難易度に偏りは無いか。などを読み取れます。